Numpy 隨機數

隨機數生成

AI 中的隨機數可以用來初始化模型的權重，這樣每次訓練模型時可以有不同的結果。隨機數生成是神經網絡訓練的一個重要部分。

np.random.rand(10) ：
這個函數會生成 10 個隨機浮點數，每個數值都在 0 和 1 之間。

小專題：輔仁大學學生人數預測

用線性回歸模型預測輔仁大學在未來幾年的學生人數變化，並利用 Numpy 進行數據運算。

程式碼總覽

解題分析

1. 數據準備

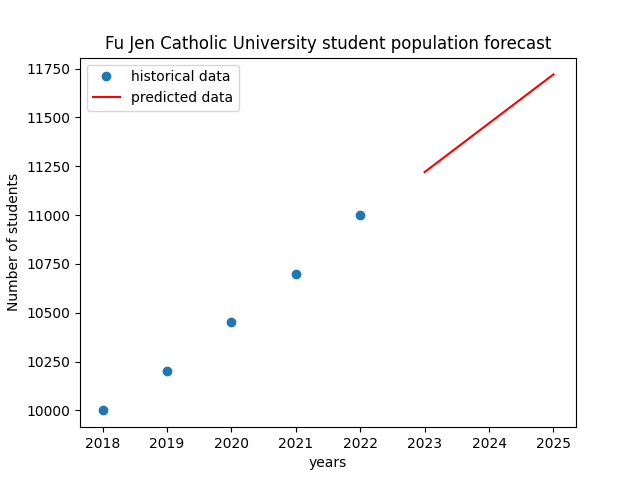
首先要準備一些歷史的學生人數數據，比如說從 2018 年到 2022 年，每年輔仁大學的學生數量分別是這樣：

把每一年的數據輸入到 Numpy 陣列中。years 是年份，students 是那一年輔大學生的總數。

2. 線性回歸模型的建立

假設數據是根據一條直線來變化，我們需要找出這條直線的方程式，也就是：y = ax + b。這裡 a 是斜率，b 是截距。這條直線能幫助我們用過去的數據來預測未來。

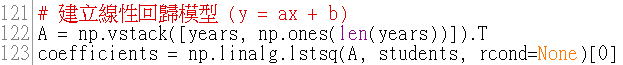
• np.vstack([years, np.ones(len(years))]).T：
  這個步驟是把年份和一個全是 1 的數組堆疊在一起，這樣就能構建出我們的線性方程式的系統。

  np.vstack() 是垂直堆疊的意思。它把 years 和全是 1 的數組堆疊在一起，形成一個 2xN 的矩陣，第一行是年份，第二行是全 1。例如，如果 years = [2023, 2024, 2025]，那麼堆疊後的結果是：
  [[2023, 2024, 2025],
  [1, 1, 1]]

  最後的 .T 是 轉置矩陣，把原來 2xN 的矩陣變成 Nx2 的矩陣。這樣的變換是為了符合矩陣運算的需求，準備後面進行回歸計算。轉置後的結果是：
  [[2023, 1],
  [2024, 1],
  [2025, 1]]
  這個矩陣代表了線性方程式中的輸入數據，其中每一列是用來計算 y=mx+c 的變量：第一列是年份 x，第二列是常數項 1，用來乘以截距 c。

• np.linalg.lstsq：
  這是 Numpy 用來求解最小平方解法的函數，這個函數會幫我們找到那條最接近數據的直線。coefficients[0] 是斜率 a，coefficients[1]：是截距 b。

3. 預測未來的學生人數

有了模型後，我們就可以用它來預測未來幾年的學生人數了~這裡我們選了 2023 年到 2025 年，然後套用剛剛算出來的方程式：

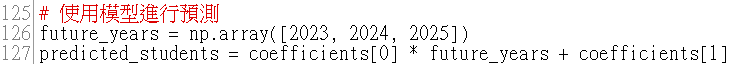
這段程式碼會用剛剛計算出的斜率 a 和截距 b，來預測 2023、2024 和 2025 年的學生人數。

4. 畫圖表

最後可以把結果畫出來，這樣我們不只是在數字上看預測，也能夠用圖表來清楚了解趨勢：

• plt.plot(years, students, 'o')：
  畫出過去的歷史數據，用小圓點表示。
• plt.plot(future_years, predicted_students, 'r-')：
  畫出預測數據，用紅色的線來表示未來幾年的趨勢。

結語

在學習 Numpy 模組的隨機數後，我了解到隨機數在很多AI應用中扮演了重要角色，特別是在資料分析、機器學習的模型訓練和模擬中。隨機數能幫忙生成不同情境的資料，進而提升模型的泛化能力。

在做輔仁大學學生人數預測的小專題時，我使用了線性回歸模型來預測之後的學生人數。因為把很理論的東西應用在現實生活當中，讓我更能理解它的用法，不再只是操作很死板的數學運算。

而最後也順便複習到了之前有學習過的圖表設計，把數據可視化，更提升了我的數據整理能力><